Při řešení řady úloh na počítači jste postaveni před úkol vyřešit soustavu několika lineárních rovnic o několika neznámých.
Příkladem může být prodej několika komodit v různých regionech, kdy znáte celkové tržby a prodaná množství, ale neznáte ceny komodit. U prvého regionu zřejmě platí:
Tržba v regionu 1 = Množství komodity 1 prodané v regionu 1 * Cena komodity 1 + …
Obdobné rovnice platí u dalších regionů. Abyste nalezli ceny jednotlivých komodit, musíte vyřešit tuto soustavu rovnic, tj. nastavit jednotlivé ceny tak, aby byly tyto rovnice splněny.
Pro rozsáhlejší soustavu, obsahující více než tři rovnice se jedná o poměrně složitý problém, který však můžete poměrně zvládnout pomocí funkcí Excelu.
Soustavu lineárních rovnic typu
a11x1 + a12x1 + … = b1
a21x1 + a22x2 + … = b2
je možné zapsat také jako součin dvou oblastí buněk:
A*x = b
Po vydělení této rovnice maticí A, což ji převede na tvar
x = A-1*b
je problém vyřešen.
Výpočet matice A-1, která se označuje jako inverzní matice, provádí v Excelu funkce INVERZE, která je zařazena do skupiny „Matematické“.
Funkce INVERZE má jediný parametr „Pole“, kterým je zpracovávaná matice. Výsledkem funkce je matice téže velikosti. Proto musíte před použitím funkce INVERZE označit potřebnou oblast buněk a vložení vzorce s funkcí INVERZE potvrdit pomocí tlačítka OK s podrženými klávesami Ctrl a Shift nebo klávesovou kombinací Ctrl + Shift + Enter.
Jestliže na to zapomenete, výsledek se dosadí jen do jediné buňky. Pokud označíte méně buněk, vypočítá se jen část inverzní matice. Jestliže naopak označíte více buněk, než odpovídá vstupní oblasti, zbytek buněk bude vyplněn hodnotami „#N/A“.
Výsledkem funkce INVERZE je oblast buněk (matice). V této oblasti není možné mazat nebo přepisovat jednotlivé buňky. K odstranění vytvořeného vzorce je zapotřebí označit celou oblast a smazat ji najednou.
K úpravě vzorce s funkcí INVERZE musíte opět označit všechny buňky s výsledky, provést potřebnou úpravu a vložení potvrdit opět s podrženými klávesami Ctrl a Shift nebo kombinací Ctrl + Shift + Enter.
Při použití funkce INVERZE musíte dbát na následující zásady:
- Vstupní oblast buněk musí být čtvercová (stejný počet řádků a sloupců).
- Oblast nesmí obsahovat textové hodnoty.
- Prázdné buňky nejsou chápány jako nuly, nýbrž jako chybný vstup.
Při porušení některé z těchto zásad vrátí funkce INVERZE chybovou hodnotu „#HODNOTA!“. Aby bylo možno funkcí INVERZE vypočítat inverzní matici, nesmí být determinant vstupní matice nulový.
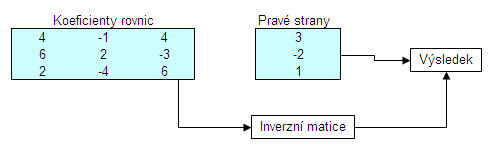
Po výpočtu inverzní matice je dalším krokem násobení této matice sloupcovou oblastí buněk, obsahující pravé strany řešené soustavy lineárních rovnic.
K tomu použijete funkci SOUČIN.MATIC, kterou naleznete ve skupině „Matematické“. Do prvního parametru funkce „Pole1“ vyznačíte oblast s vypočítanou inverzní maticí a do druhého parametru „Pole2“ sloupec buněk s pravými stranami soustavy rovnice.
Výsledkem výpočtu je sloupec hodnot, obsahují jednotlivé hledané neznámé. Protože funkce SOUČIN.MATIC vrací oblast hodnot, při tvorbě vzorce s touto funkcí postupujete stejně jako u funkce INVERZE.
Nejprve vyznačíte oblast buněk pro výsledky, potom provedete vložení funkce SOUČIN.MATIC a výsledný vzorec potvrdíte tlačítkem OK s podrženými klávesami Ctrl a Shift nebo klávesovou kombinací Ctrl + Shift + Enter. U výsledných buněk opět není možné změnit pouze část vytvořeného vzorce.
Všechny soustavy lineárních rovnic však nelze popsaným způsobem vyřešit. Jestliže je determinant vstupní matice roven nule, soustava nemá řešení. V takovém případě však vrátí chybovou hodnotu již vzorec pro výpočet inverzní matice pomocí funkce INVERZE.